Introduction to Neurons, Backpropagation and Transformers
This is a companion article to ‘General Theory of Neural Networks’
Artificial Neural Networks are a profound discovery. Both philosophically and scientifically, they’re more than tools for creating powerful language models. I believe artificial neural networks will have a similar effect on our understanding of physics, reality, and intelligence as the theory of evolution had on biology. As the evolutionary biologist Theodosius Dobzhansky once wrote, "Nothing in Biology Makes Sense Except in the Light of Evolution."
Recognition of a pattern precedes scientific inquiry. We first interpret these patterns through philosophy or craft. Only later, with a concrete mathematical framework, do they become science and engineering. Much of what I’ll discuss in future essays is still philosophical, but the goal is to take us closer to science.
However, before we get into a General Theory of Neural Networks in the next essay, it’s necessary to introduce the basic concepts of artificial neural networks, training, and GPTs which are beginning to cross the boundary of open-endedness similar to other biological networks utilizing this basic architecture.
Biological Neurons
The term "neuron" was coined by German anatomist Heinrich Wilhelm Waldeyer in 1891, based on early work by Santiago Ramón y Cajal and Camillo Golgi, whose work established the Neuron Doctrine. This doctrine proposed that neurons are discrete, individual cells that communicate through synapses. By the early 20th century, it was understood that neurons transmit electrical impulses and chemical signals. Neurons consist of a cell body (soma), dendrites, and axons. Dendrites are fibers that receive signals and conduct them toward the soma, and an axon is another fiber that carries impulses away from the soma to other neurons or effector cells. The junction where the axon (output) from one neuron connects to a dendrite (input) of another neuron is called a synapse.
Here are the basic dynamics of neurons:
Reception: Dendrites receive chemical signals from other neurons.
Transmission: These chemicals cause electrical changes in the dendrite, creating signals that move toward the cell body.
Integration: The cell body adds up all incoming signals. If they’re strong enough, an electrical signal (action potential) is generated.
Propagation: This action potential travels down the axon to the end of the neuron which branches out to other dendrites..
Communication: The action potential triggers the release of chemicals (neurotransmitters) at the synapse, passing the signal to the next neuron.
McColloch Pitts Neuron and the Perceptron
In 1943, Warren McCulloch and Walter Pitts published a paper introducing a mathematical model of neural networks. Their goal was to understand and formalize how neural processes could give rise to complex behaviors and cognitive functions. They aimed to bridge the gap between neuroscience and logical computation by demonstrating that neural activity could be represented through logical expressions and computations. Their work laid the foundation for modern computational neuroscience and artificial intelligence.
Building on this foundation, Frank Rosenblatt introduced the perceptron in 1958, which became the simplest form of an artificial neural network. The perceptron directly models the concept of a neuron as a computational unit, taking several inputs and producing a single output.
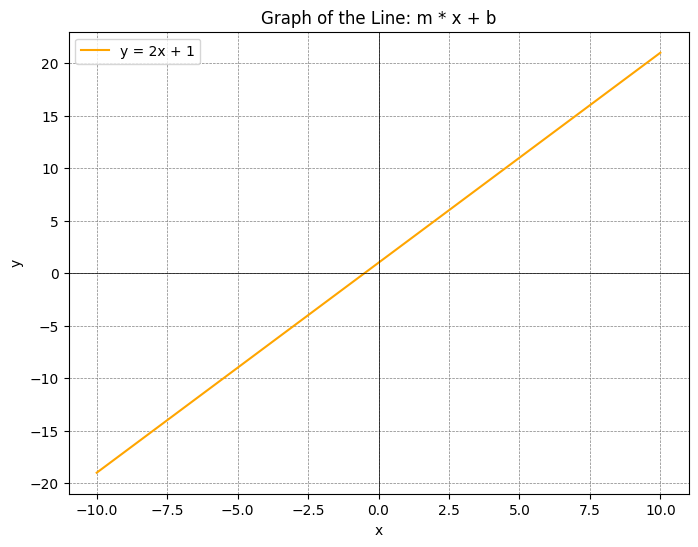
Today, neurons (or perceptrons in artificial networks) are fundamental units of computation in artificial intelligence. Mathematically, a neuron is a function that takes multiple inputs, applies a weighted sum, and then passes the result through an activation function to produce an output. The basic structure is given as:
Where xj is the output activity from neuron j, wkj denotes the strength and sign of the interaction from neuron j to neuron k, and (x) is a non-linear activation function.
In the simplest perceptron model with binary weights (0,1) or bipolar (-1, 1) the activation function is a step function, outputting 1 if the weighted sum exceeds a threshold and 0 otherwise. However, modern neural networks often use more complex activation functions like ReLU, Tanh, or Sigmoid, which we'll discuss shortly.
If you squint a little at the inner expression, you’ll notice that with only one input (n = 1), you get the equation for the line y = mx + b, a function that maps values of x to values of y. Conceptually, the slope m is a multiplier that tells you how much to amplify the input signal xj, and the intercept b is a bias tells you the value of y when x = 0.
Translating the equation of the line to neural networks, xj is the activation intensity coming from neuron j; wij indicates how much to amplify the signal from neuron xj going to neuron yk; and the bias (b) determines how sensitive the activation function of neuron yk is to its input signals. When there are many input neurons, Sigma (Σ) just sums up the individual contributions from each input neuron, and a single bias is added at the end. This sum is then fed into a threshold activation function such as ReLU, Tanh, or the Sigmoidal function.
The threshold function adds non-linearity, meaning it helps the network understand more complicated data. Without it, the network could only handle simple, straight-line relationships. Common activation functions include ReLU (which turns on for positive inputs) and sigmoid (which squashes values between 0 and 1). Here are for examples of threshold functions below.
You’ll notice that all these functions have a lower asymptote and with the exception of ReLU, they all have an upper asymptote. Outside a narrow band of inputs around zero this tends to result in a binary outcome.
Boolean Networks
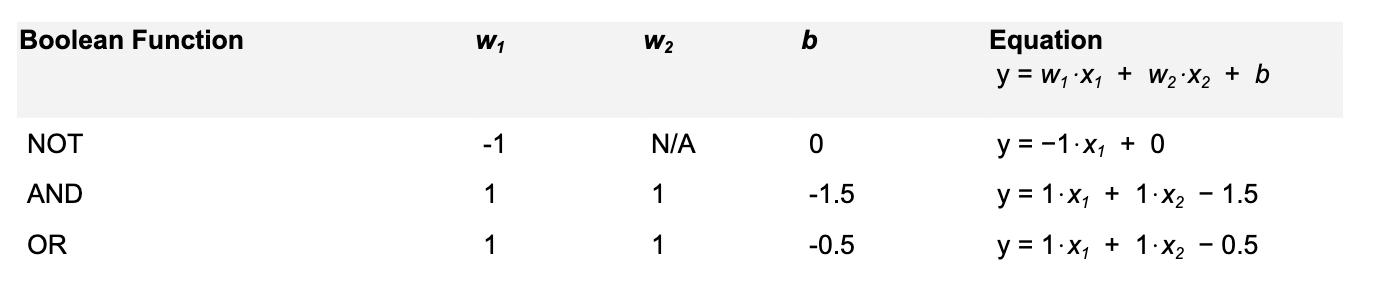
For reference in the proceeding essay, I also want to point out that neurons can also combine to represent boolean functions.
Importantly, the set of boolean functions AND, OR, and NOT together are also Turing complete. A set of Boolean functions is Turing complete if you can use it to represent any possible Boolean function through combinations of these functions. In other words, you can build a universal computer that can perform any computation that can be described algorithmically and it’s the foundation for the development of general-purpose programming languages and computers.
Training Networks: Back Propagation
Backpropagation has been a key algorithm used to train neural networks. It adjusts the weights of connections in the network to minimize the difference between the actual output and the desired output. Here’s how it works in simple terms:
Forward Pass: The input data is passed through the network, layer by layer, to generate an output. This could be a single number or a sequence of numbers. This output is compared to the actual target, and the error (difference between actual and desired output) is calculated.
Error Calculation: The error is measured using a “loss function”. which quantifies how far off the network's predictions are from the actual values. Common loss functions include Mean Squared Error (MSE) for regression tasks and Cross-Entropy Loss for classification tasks. Let’s take a quick look at Mean Squared Error:
This can look a bit scary if you haven’t taken statistics, but if you step back you see we're just adding squares. And adding squares looks a lot like Phythageom theorem a2 + b2 = c2 when you just have two values. So you can think of Mean Squared Error as computing the hypotenuse of the triangle. And just like a triangle, when sides a and b get larger in different dimensions, the hypotenuse also gets proportionally larger, which we can interpret as a greater error. The inner term being squared is just the output value (yi) subtracted by the target value (yi hat). The bigger the difference between the output and the target, the bigger this term will be and the more it will contribute to error. The sum of squares is then averaged by the number of comparisons to normalize the result.
Backward Pass: The error is propagated back through the network. This involves calculating the gradient of the loss function with respect to each weight in the network. This gradient tells us how much a change in each weight will affect the loss.
Weight Update: Using the gradients, the weights are adjusted to reduce the error. This is typically done using an optimization algorithm like Gradient Descent, which updates each weight in the direction that reduces the loss. You can think of this as countersteering when a vehicle swerves, where you turn the steering wheel in the opposite direction of the swerve to regain control of the vehicle.
By repeatedly passing data forward and propagating the error backward, the network gradually learns the optimal weights that minimize the loss, thereby improving its performance on the given task.
From Single Neurons to Multi-Layer Perceptrons
While individual neurons (or perceptrons) are interesting computational units, their capabilities are limited. As Marvin Minsky and Seymour Papert demonstrated in 1969, single-layer perceptrons can only solve linearly separable problems. This limitation led to the development of Multi-Layer Perceptrons (MLPs), also known as feedforward neural networks.
MLPs consist of multiple layers of neurons:
Input Layer: Receives the initial data.
Hidden Layer(s): One or more layers between the input and output, where most of the computation occurs.
Output Layer: Produces the final result.
Each neuron in one layer is connected to every neuron in the subsequent layer, forming a fully connected network. This architecture allows MLPs to approximate any continuous function, overcoming the limitations of single-layer networks.
The power of MLPs lies in their ability to learn hierarchical features. Lower layers typically learn simple, low-level–more granular–features from the data, while higher layers combine these to recognize more complex, abstract patterns. This hierarchical learning is a key factor in the success of deep learning.
MLPs are trained using the backpropagation algorithm, adjusting the weights across all layers to minimize the error between predicted and actual outputs. This process allows the network to learn intricate patterns in data, making MLPs applicable to a wide range of tasks, from simple classification problems to complex regression and pattern recognition tasks.
However, while MLPs are powerful, they have limitations. They struggle with sequential data and can't easily capture spatial relationships in data. These limitations led to the development of more specialized architectures like Convolutional Neural Networks (CNNs) for image processing and Recurrent Neural Networks (RNNs) for sequential data.
Types of Artificial Neural Networks
While we've focused on Multi-Layer Perceptrons (MLPs) and Transformers, it's important to note that there are several other types of neural networks, each designed to tackle specific kinds of problems:
Convolutional Neural Networks (CNNs): Inspired by the visual cortex, CNNs excel at processing grid-like data, such as images. They use convolutional layers to detect local patterns and pooling layers to reduce dimensionality. CNNs have revolutionized computer vision tasks like image classification and object detection.
Recurrent Neural Networks (RNNs): Designed to handle sequential data, RNNs have connections that form cycles, allowing information to persist. They're particularly useful for tasks involving time series or natural language. However, they can struggle with long-term dependencies.
Long Short-Term Memory Networks (LSTMs): A special kind of RNN designed to address the vanishing gradient problem in standard RNNs. LSTMs can learn long-term dependencies and have been successful in tasks like language modeling and speech recognition.
Generative Adversarial Networks (GANs): Consist of two neural networks—a generator and a discriminator—that are trained simultaneously through adversarial training. GANs are particularly good at generating new, synthetic data that resembles the training data, and have applications in image generation and style transfer.
Autoencoders: These networks are trained to reconstruct their input, forcing them to learn efficient encodings of the data. They're useful for dimensionality reduction, feature learning, and generating data.
Each of these architectures has its strengths and is suited to different types of tasks. The development of Transformer models, which we'll explore next, represents another significant leap in neural network architecture, particularly for processing sequential data like language.
These specialized architectures have all contributed to the advancement of AI in various domains. However, the introduction of Transformer models, which we'll explore next, represents another significant leap in neural network architecture, particularly for processing sequential data like language.
From Neural Networks to GPTs: The Power of Attention
While traditional neural networks laid the groundwork for modern AI, a revolutionary concept called the attention mechanism has become the cornerstone of some of the most powerful language models today, including GPTs (Generative Pre-trained Transformers).
The attention mechanism is the key innovation that distinguishes GPTs from earlier neural networks:
Global Context: Unlike earlier models that process data sequentially or in fixed-size windows, the attention mechanism allows the model to consider the entire input simultaneously, weighing the relevance of every element for each prediction.
Dynamic Focus: Attention enables the model to dynamically focus on different parts of the input depending on the current context, mimicking the human ability to concentrate on relevant information while ignoring the irrelevant.
Parallelization: This approach enables much more efficient parallel processing, allowing for training on vastly larger datasets and scaling to billions of parameters.
Long-range Dependencies: The attention mechanism excels at capturing long-range dependencies in data, crucial for understanding context in language and solving complex reasoning tasks.
Building on the attention mechanism, researchers developed a new type of language model called GPT (Generative Pre-trained Transformer). GPT models are designed to predict the next word in a sequence, much like how we might guess the next word in a sentence. As each new word is generated, it’s added to the original input sequence to generate the next word, until it generates a token telling the GPT to stop generated. This approach, known as autoregressive modeling, allows GPTs to generate coherent and contextually appropriate text. Strictly speaking, GPTs are feed-forward networks, but feeding the output back into the input layer creates a recurrent feedback structure, and therefore the potential for open-endedness.
GPT models implement this attention mechanism within a specific neural network structure. This structure, inspired by earlier designs called transformers, processes information sequentially, similar to how we read text from left to right. Each part of the input (like a word in a sentence) is processed in light of all the parts that came before it, allowing the model to maintain context throughout long sequences of text.
GPT models leverage this attention mechanism and several other recent advancements. Let's explore the key components that make GPTs so powerful:
Word Embeddings: High-dimensional vector representations of individual words based on semantic relationships.
Transformer Architecture: GPT uses the decoder portion of the original transformer architecture.
Self-Attention Mechanism: This allows the model to weigh the importance of different parts of the input when processing each token.
Multi-Head Attention: Multiple attention mechanisms run in parallel, allowing the model to focus on different aspects of the input simultaneously.
Feed-Forward Neural Networks: These process the output of the attention layers.
Large-Scale Pre-training: GPT models are pre-trained on vast amounts of text data.
Autoregressive Nature: The model predicts the next token based on all previous tokens.
Scalable Architecture: The basic structure can be scaled up by adding more layers and increasing model size.
GPTs are monolithic which makes them hard to comprehend, but the overall structure is relatively simple if you can push through. In particular, understanding the vector embeddings and the mechanics of the attention mechanism are tricky, and I recommend several excellent videos that can help with visualization and more concrete examples:
Visual Guide to Transformer Neural Networks - (Episode 2) Multi-Head & Self-Attention
The math behind Attention: Keys, Queries, and Values matrices
I’ll give a brief description of the major concept below:
High-dimensional Vector Embeddings: Tokens, which are words or parts of words, are represented as long vectors of floating point numbers, together representing a position in high-dimensional space. For instance, in GPT-2, each token is represented by a vector with 1,600 dimensions. A word like "mole" would be represented as a vector of 1,600 numbers, one number for each dimension. Absent context, however, the token <mole> could mean various things: a group of atoms, an animal, a spot on someone's face, or a spy. This initial semantic ambiguity is important as we’ll see below.
Embedding Space: During training, the AI learns the semantic relationships between tokens by adjusting the values in each token’s embedding vector. This process moves words around in high-dimensional space, clustering tokens with similar attributes together in a subset of dimensions. For example, the tokens <lion> and <house cat> would be closer to each other than to <pitbull> in those dimensions semantically associated with <cat>, while <house cat> and <pitbull> would cluster closer together in dimensions semantically associated with <pet>. Similarly, values in one or two dimensions may relate to other attributes such as size, color, or mood.
Visualizing Embeddings: To simplify their visualization, imagine tokens represented by a 2-dimensional embedding vector (x, y). Each token is plotted at its x-y position, and the similarity between tokens is measured by the dot product of their vectors. The dot product indicates whether tokens are close (positive value) or far apart (negative value) in this space. A value close to zero suggests orthogonality, meaning the tokens have no significant similarity in those dimensions. Another way to compare similarity is the cosine similarity between the vectors. When the cosine angle between two points from the origin is similar, then the tokens are semantically similar.
Attention Heads: Attention heads are a key component of the transformer architecture, first introduced in the 2017 paper Attention is All You Need. Attention heads provide the context for the word embeddings in a sequence. For example, given the sequence: “The mole on her face” the tokens <her> and <face> provide context (attend to) the token <mole>. In this context, <mole> most likely refers to a dark growth. However, if the sequence continued: “The mole on her face bit her nose” the token <bit> would attend to <mole>, shifting its semantic meaning to more probabilistically indicate a small furry animal.
In each layer of the transformer, are many attention heads. Each attention head processes all the tokens in the input sequence by computing ‘attention scores’ which indicate how much focus should be given to each token relative to every other token in the sequence. Through the training process, attention heads spontaneously learn to focus on different attributes and relationships–different subsets of embedding dimensions– in the sequence, enabling the transformer as a whole to capture complex relationships and dependencies within the data. Operationally, an attention head acts like a force that nudges a token’s position from a less defined representation to a position in embedding space that with more specific semantic meaning. In the example earlier, <mole> one attention head might nudged the token closer to <face> along a subset of dimensions, while <bit> might nudge <mole> closer to <animal> along another set of dimensions. Similarly, given the token <The Eiffel Tower>, multiple attention heads might work together to reposition the token’s embedding vector to something more specific like “The diecast Eiffel Tower keychain in my desk drawer”.
Once all the attention heads update a copy of their own versions of the embeddings in the sequence, they’re all integrated into a feed-forward perceptron network, and then passed up through subsequent layers of the transformer (each with its own attention heads), allowing the model to build increasingly sophisticated representations of the input. For example, the first layer may focus on basic relationships between words, while attention heads farther up may focus on complex relationships. This process continues until the final layer, where the model generates its prediction for the next token.
At the top layer, the final token embeddings predict the next token using a softmax function over the model's vocabulary. Basically giving a biased probability for the next token over the entire vocabulary.
The generated token is added to the sequence, and the whole process starts over again with the raw embeddings. This process continues, until the transformer generates an End of Sentence token ( <EOS>), telling the transformer to halt.
Here’s how the attention mechanism works step-by-step:
I Transforming Tokens:
For each token Ei in the conversation history, each attention head creates two new vectors, called the Query (Qi) and Key (Ki) vectors. These are generated using learned weight matrices 𝑊𝑄 and 𝑊𝐾, which were trained along with the rest of the model. Typically the Qi Ki vectors will be much lower dimension than the embedding vector (For example 1,600 →128), which allows the attention head to focus only on those dimensions that are relevant for this particular attention head.II Finding Similarities:
Prior to training, the 𝑊𝑄 and 𝑊𝐾 matrices for each attention head are initialized randomly. During the training regime, the network will functionally evolve to phase lock on values for 𝑊𝑄 and 𝑊𝐾 that represent a common subset of relevant dimensions, masking out non-relevant dimensions. Calculating the dot product between their Query and Key vectors measures how similar the tokens are in a subset of dimensions of the embedding space.
With the dot product, we can effectively calculate the angle between any two vectors in this lower-dimensional space, known as cosine similarity. Tokens with similar meanings will have vectors pointing in similar directions (small angle), while dissimilar tokens will have vectors pointing in different directions (large angle).
III Computing Attention Scores:After calculating the cosine similarity, the scores are scaled and passed through a softmax function to turn them into attention weights. Where cosine similarity between to tokens is high, the attending token will have more influence pulling the token it’s attending to with greater probability than other competing tokens. For instance in the sentence “Big elephant small mouse” the tokens <big> attending to <elephant> might get an exponentially high attention score (e.g. p = 0.9) while <small> attending to <elephant>, gets a lesser weight (e.g. p = 0.1). These weights are probabilities that determine how much focus the model should give to each token relative to the others.
IV Weighted Sum of Values:Each token in the sequence Ei also has a Value vector (Vi), which is generated from the transformation of the original Ei using a learned matrix 𝑊𝑉. The pair-wise attention weights for each pair of tokens are used to create a weighted sum of these Value vectors. This weighted sum is the new representation of the token Ei’ incorporating information from all other tokens based on their relevance. The effect of this is to nudge a token’s position in embedding space in such a way that its semantic meaning becomes more definite as the context evolves. For instance, if I start a conversation with “The mole” the <mole> token could refer to an animal, a group of atoms, a mole on someone's face, a spy, or Mexican sauce. However, as the context evolves new information will give tokens more context, resolving the token to a more precise meaning.